The Truth About Sarah Winchester

The Belle of New Haven

Her birth name was Sarah Lockwood Pardee. She was the fifth of seven children born to Leonard Pardee and Sarah Burns. There are no existing records or any other form of factual information to establish Sarah’s date of birth—even the year remains unknown. The scarce information that survives from the historical record indicates her birth must have occurred somewhere between 1835 and 1845.

At the time of Sarah’s birth, the Pardee’s were a respectable, upper middle class New Haven family. Her father Leonard was a joiner by trade whose shrewd sense of business found him moving up the ladder of polite society as a successful carriage manufacturer. Later, during the Civil War, he made a fortune supplying ambulances to the Union Army.

Young Sarah’s most distinguishing characteristic was that she was everything but ordinary. Like Francis Bacon, she was a child prodigy. Moreover, by all accounts, she was also considered to be quite beautiful. By the age of twelve, Sarah was already fluent in the Latin, French, Spanish, and Italian languages. Furthermore, her knowledge of the classics (most notably Homer and Shakespeare) along with a remarkable talent as a musician was well noticed. It is no wonder that New Haven Society would eventually dub her “The Belle of New Haven.”

In addition to Sarah’s brilliance and respectable place in society, there were several factors about New Haven that presented a unique influence on her upbringing. To begin, there was Yale University (originally known as Yale College). From its inception, Yale (and New Haven) was a hub of progressive, Freemasonic-Rosicrucian thinking and activity. As a result, Sarah was raised and educated in an environment ripe with Freemasonic and Rosicrucian philosophy. Several of Sarah’s uncles and cousins were Freemasons. But more importantly, at an early age, she was admitted to Yale’s only female scholastic institution known as the “Young Ladies Collegiate Institute.” Two of the school’s most influential administrators and professors, Judson A. Root and his brother N.W. Taylor Root were both Rose Croix Freemasons. In addition to the liberal arts, the Roots set forth a strict curriculum consisting of the sciences and mathematics.

Furthermore, two of Sarah’s schoolmates Susan and Rebecca Bacon were the daughters of New Haven’s highly respected Reverend Dr. Leonard Woolsey Bacon (no relation to Francis Bacon). While Sarah and the Bacon girls were attending the school, Dr. Bacon’s sister Delia, also a New Haven resident, attracted considerable fame and attention for writing her famous treatise that Sir Francis Bacon (with the aid of a circle of the finest literary minds of the Elizabethan-Jacobean Age) was the actual author, editor, and publisher of the original works of Shakespeare. Her work was sponsored by the author Nathaniel Hawthorne and was later supported by the likes of Ralph Waldo Emerson and Mark Twain. In addition to her writing, Delia Bacon gave numerous public lectures to the citizens of New Haven; thus, New Haven, Connecticut was the actual birthplace of the “Bacon is Shakespeare” doctrine.

Given her direct exposure to the Baconian Doctrine, along with her passion for the Shakespearean works, it was inevitable that Sarah Pardee was drawn like an irresistible force to a more than passing interest in the new theorem. Moreover, the Baconian-Masonic preoccupation with secret encryption techniques using numbered cipher systems most certainly influenced young Sarah’s world view. This unique backdrop to Sarah’s early development played a crucial role which, in essence, defined what would become her life’s work.

As we shall see, the Belle of New Haven became a staunch Baconian for the rest of her life. She also acquired a vast and uncanny knowledge of Masonic-Rosicrucian ritual and symbology. Additionally, she gravitated to Theosophy. Author and historian Ralph Rambo (who actually knew Sarah) wrote “it is believed that Mrs. Winchester was a Theosophist.” Rambo didn’t elaborate on the matter, but since he was close to Sarah he was certainly in a position to know some things about her. It should be noted that most Rosicrucians are theosophists.

Sarah adhered both to Bacon’s Kabbalistic theosophy and the theosophical perspective held by Rudolph Steiner (1861- 1925). Steiner viewed the universe as a vast, living organism in which all things are likened to individually evolving units or cells that comprise a greater universal, synergistic body that is “ever building.” As we shall further see, the “ever building” theme was at the core of Sarah’s methodology.

William and Annie

William Wirt Winchester was born in Baltimore, MD on July 22, 1837. He was the only son of Oliver Fisher Winchester and Jane Ellen Hope. In keeping with a popular trend of the day, he was named after William Wirt, the highly popular and longest serving Attorney General of the United States .

Soon after William’s arrival, the Winchesters moved to New Haven where the enterprising Oliver, along with his partner John Davies, founded a successful clothing manufacturing company. Gradually, the Winchester patriarch amassed a considerable fortune. Later, Oliver channeled his efforts into a firearms manufacturing venture that eventually (1866) evolved into the famous Winchester Repeating Arms Company.

According to historical documents, the Winchesters and the Pardees were well acquainted, particularly through the auspices of New Haven’s First Baptist Church. Additionally, Sarah Pardee and William’s sister Annie were classmates at the Young Ladies Collegiate Institute.

Not far away, William attended New Haven’s Collegiate and Commercial Institute—another arm of Yale College. Here, William’s teachers included N.W. Taylor Root (one of Sarah’s instructors) and Henry E. Pardee who was another of Sarah’s cousins. Thus, Young Sarah and William found themselves studying virtually the same curriculum under very similar circumstances. Moreover, like the Pardees, the Winchester family was not lacking in members who were Freemasons.

Sarah and William were married on September 30, 1862. Their only child, Annie Pardee Winchester came into the world on July 12, 1866. Unfortunately, due to an infantile decease known as Marasmus (a severe form of malnutrition due to the body’s inability to metabolize proteins), Annie died 40 days later.

In 1880, Oliver Fisher Winchester died, leaving the succession of the Winchester Repeating Arms Company to his only son. One year later, William died of Tuberculosis at the age of 43. The double loss of Annie and William was a staggering blow to Sarah. However, the loss did leave the widow Winchester with an inheritance of 20 million dollars plus nearly 50% of the Winchester Arms stock—which, in turn earned her approximately $1,000 dollars per day in royalties for the rest of her life—the result of which made her one of the wealthiest women in the world.

Europe and California

According to Ralph Rambo, Sarah went on a three year world tour before settling in California in 1884. “The New Haven Register,” dated 1886, lists Sarah as having been “removed to Europe.” No other information has survived to tell us exactly where Mrs. Winchester went during those years or what her activities consisted of. But we can project some well educated theories.

Although Freemasonry has traditionally barred women from its membership, there are numerous documented cases in which some head-strong women have gained admittance into liberal, Masonic Lodges as far back as the 18th Century. A movement in France called Co-Freemasonry, which allows for male and female membership was already underway when Sarah arrived in that country. Given her social status, a predilection towards Freemasonic tenets, and a mastery of the European languages, Sarah could easily have been admitted into any of the permissive French Masonic lodges.

Another possible scenario involving Mrs. Winchester’s activities while abroad could well have included visits to esoteric, architectural landmarks such as the French Cathedral of Chartres. Sarah’s Masonic-Rosicrucian interest in labyrinths would have drawn her to Chartres with its 11 circuit labyrinth, a puzzle-like feature that stresses the discipline of the initiatic tradition of the ancient mystery schools. Likewise, she would also have found inspiration in the Freemasonic symbology and the mysterious structure (including a staircase that leads nowhere) of Rosslyn Chapel in Scotland .

In 1884, Sarah took up residence in the San Francisco Bay area—eventually moving inland to the Santa Clara Valley (now San Jose) to buy an eight room farmhouse from one Dr. Robert Caldwell. Her apparent motive for the move was to live in close proximity to her numerous Pardee relatives, most of whom had come to California during the 1849 Gold Rush, and were scattered from Sacramento to the Bay area.

One of these Pardee relatives, Enoch H. Pardee, had become a highly respected physician and politician while living in Oakland. Later his son George C. Pardee followed in his father’s footsteps rising to the office of Governor of California (1903- 1907.

It is interesting that Wikipedia makes particular note of Enoch Pardee having been “a prominent occultist.” Most likely the occult reference has to do with the fact that both Enoch and his son George were members of the highly secretive and mysterious ( California based) Bohemian Club which was an offshoot of Yale’s Skull and Bones Society. Moreover, Enoch and George were Knights Templar Freemasons.

Also interesting, is the fact that President Theodore Roosevelt (another member of the Bohemian Club) came to California in 1903 to ask Governor Pardee to run as his Vice Presidential candidate in the 1904 national election. The offer was turned down. During the same trip, Roosevelt attempted to visit Sarah Pardee Winchester. Again, Roosevelt’s offer was turned down.

The House

After purchasing Dr. Caldwell’s house along with its 161 acres of farmland, Mrs. Winchester hired a crew of approximately 20 carpenters, and began the implementation of a vast, building project that lasted until her death 38 years later. The construction of the House was an “ever building” enterprise in which rotating shifts of workers labored 24 hours per day, 7 days a week, 365 days a year. With Mrs. Winchester as its’ only architect, the House gradually mushroomed outward and upward, reaching a height of 7 stories in some places, and encompassing 500 – 600 rooms. The 1906 earthquake reduced the House to 4 stories. Thereafter, Sarah refrained from venturing any higher.

Aside from its immense size and Victorian style architecture, the House has a number of unique characteristics. To begin, it is undeniably a labyrinth. There are literally miles of maze-like corridors and twisting hallways, some of which have dead ends—forcing the traveler to turn around and back-up. There are also some centrally located passages and stairways that serve as shortcuts allowing a virtual leap from one side of the House to the other. Traversing the labyrinth is truly dizzying and disorienting to one’s sensibilities.

The House abounds in oddities and anomalous features. There are rooms within rooms. There is a staircase that leads nowhere, abruptly halting at the ceiling. In another place, there is a door which opens into a solid wall. Some of the House’s 47 chimneys have an overhead ceiling—while, in some places, there are skylights covered by a roof—and some skylights are covered by another skylight—and, in one place, there is a skylight built into the floor. There are tiny doors leading into large spaces, and large doors that lead into very small spaces. In another part of the House, a second story door opens outward to a sheer drop to the ground below. Moreover, upside-down pillars can be found all about the House. Many visitors to the Winchester mansion have justifiably compared its strange design to the work of the late Dutch artist M.C. Escher.

Door to nowhere

Stairs to nowhere

Skylight embedded in the floor

The Front of the Winchester Mansion

Adding further to the mysterious features, the prime numbers 7, 11, and 13 are repeatedly displayed in various ways throughout the House—the number 13 being most prominent. These numbers consistently show up in the number of windows in many of the rooms, or the number of stairs in the staircases, or the number of rails in the railings, or the number of panels in the floors and walls, or the number of lights in a chandelier, etc. Unquestionably, these three prime numbers were extremely important to Sarah (and to Francis Bacon).

Well ahead of her time, Mrs. Winchester employed many high tech inventions of her day. She is believed to have been the first builder to use of wool insulation. The House was lit with carbide gas lights that were supplied by its own gas manufacturing plant. Panels of electric buttons were used to operate the lights by means of electro-mechanical strikers that caused a spark to ignite the various lamps. Sarah was also among the first to make use of a shower—and elevators, two driven by hydraulics, and a third by electricity.

Practically a small town unto itself, the Winchester estate was virtually self sufficient with its own carpenter and plumber’s workshops along with an on-premise water and electrical supply, and a sewage drainage system.

News of Mrs. Winchester’s death (September 5, 1922) found her workers halting construction—leaving nails half driven into the walls.

In accordance with her twelve page 13 part will (signed by her 13 times), Sarah had her entire estate divided up in generous portions to be distributed among a number of charities and those people who had faithfully spent years in her service. Her favorite niece and secretary, Marian Marriott, oversaw the removal and sale of all of Sarah’s furnishings and personal property. Roy Lieb, Mrs. Winchester’s attorney of many years, had been named in her will as executor to her estate. He sold the House to the people who, in 1933, preserved it as a “living” museum—today, it is known as the Winchester Mystery House also known as California Historical Landmark #868. Although no mention has ever surfaced as to any specific guidelines or special instructions by which Mr. Lieb would select a buyer for the property, one gets the distinct impression that Sarah wanted the House to stand intact and perpetually preserved… and so it does.

The Folklore

Despite the fact that Sarah Winchester was extremely secretive about herself, nearly all of what the public thinks it knows about her reads like a mish-mash of gossip out “The National Enquirer.” I refer to this body of misinformation as “The Folklore.” Indeed, on one of my many research visits to the Winchester Mystery House, a senior tour guide informed me that “in the old days, the tour guides were encouraged to make up stuff just to give some spice to the story.”

The Folklore about Sarah says that, after William’s death in 1881, the highly distraught Mrs. Winchester sought the advice of the then famous Boston medium Adam Coons. During a séance with Coons, Sarah was told that because of the many people who had been slain by the Winchester Rifle, she was cursed by the Winchester fortune. Coons further instructed Sarah that the angry spirits demanded that she move to California and build them a house.

Upon her arrival in California, Sarah began holding her own séances every midnight so that she could receive the next day’s building instructions from the spirits. Her séances allegedly involved the use of a Ouija board and planchette, and 13 various colored robes she would ritualistically wear each night (for the edification of the spirits) within the confines of her “Séance Room.”

To further appease the angry spirits, Mrs. Winchester made sure the construction of the House went on, nonstop, 24 / 7, 365 days a year for fear that should the building ever stop, she would die.

For some inexplicable reason, however, Mrs. Winchester took precautions in the building design so as to incorporate all of the strange features of the House to “confuse the evil spirits.” Moreover, she would ring her alarm bell every night at midnight to signal the spirits that it was séance time, and then again at 2:00 am, signaling the spirits that it was time to depart. Which begs the question “who was in charge of whom?” And, why would spirits’ have an inability or need to keep track of time?

Furthermore, Sarah infused the numbers 7 and 11 into the architecture because they are lucky numbers. And the number 13? Well, as everyone knows, that’s an unlucky number which Mrs. Winchester used to ward off the evil spooks. She also slept in a different room every night as an extra measure to throw the spirits off her trail.

Whenever I make mention of Sarah Winchester the typical response I get from people is “Oh yeah…wasn’t she the crazy lady who built that weird house because she was afraid the spirits would kill her?” Many of these people have never been to the Winchester House. Their source is usually television. “ America ’s Most Haunted Places” tops the list of TV shows that grossly reinforces the Folklore.

The misinformation is further compounded by the “Haunted House” tour business thriving in San Jose as the commercial enterprise known as the “Winchester Mystery House” which profits by perpetuating the Folklore myth. In fairness to the management of the “WMH,” they try to present Mrs. Winchester in a positive light. However, their Halloween flashlight tours, along with booklets, postcards, coffee mugs and other sundry items being sold in the WMH souvenir shop displaying the title “The Mansion Designed By Spirits” only enhances the Folklore version of Sarah Winchester’s life. You’ve got to hand it to them they’ve created a highly effective marketing strategy for a very lucrative commercial enterprise. These are good people who mean well—but this is hardly the legacy Sarah wanted to leave to posterity.

Dispelling the myth

As with Francis Bacon, Sarah Winchester’s legacy has fallen victim to The Liberty Valance Effect, i.e. “when the legend becomes fact, print the legend.” Fundamentally, the tour guides at the WMH know the canned patter they to feed the tourists is mostly Folklore. But why bother looking beyond the superficial “orthodox” Folklore when it’s much more convenient to embrace the myth, and keep reciting the mantra “we’ll never know what Mrs. Winchester’s thoughts and motives were.” However, historians and archeologists would sharply disagree, particularly when the person of interest has deliberately gone to great lengths to leave a well designed trail of clues and artifacts to follow. It then becomes a matter of separating fact from fiction—beginning with the elimination process.

Let’s start with the allegations about Sarah and Adam Coons. There is no record or evidence that Mrs. Winchester ever met the man. Nor is there any evidence to support the idea that she was a spiritualist or had any inclination to believe in communication with the deceased. Moreover, there is absolutely no factual basis to support the idea that Sarah ever used the so-called Séance Room for the purpose of conducting séances. Her closest companion and nurse of many years, Henrietta Severs, firmly denied that Mrs. Winchester had any spiritualist leanings.

Furthermore, why would odd features built into a house confuse evil spirits? Perhaps the better question is why would anything that is strange, or not understood have to be explained as being related to “the spirit world?”

And finally, if Mrs. Winchester truly believed she was cursed by the Winchester fortune, why would she exacerbate the matter by continuing to own vast shares of stock in the Winchester Repeating Arms Company, then, later acquire still greater controlling shares that she maintained and profited from for the rest of her life?

Unquestionably, for many people, the folklore is entertaining—but it is a complete fabrication. With regard to Sarah’s reason for building the House the way she did, author Ralph Rambo states: “The great question is yet to be answered,—Why? Why?”

Mystery Solved

Once the folklore is set aside the bare bones of Sarah’s mystery are more easy to examine. In fact, the term “mystery” is much too ethereal, implying an unreachable quality which cannot be ascertained. Sarah made certain her legacy was well within reach and capable of being understood. Therefore, like the folklore, the term “mystery” should be put aside and replaced with the more appropriate term “puzzle.” Like the Chartres Cathedral in France , or Rosslyn Chapel in Scotland , Sarah’s architectural legacy is an artful puzzle. Thus, the solution to Ralph Rambo’s question (“Why? Why?”) is a matter of connecting the dots and properly assembling the pieces of the puzzle Sarah has generously left behind. Furthermore, she began crafting her puzzle long before the construction of the House.

Encryption Codes—The Winchester-Bacon Connection

As noted earlier, young Sarah Pardee was raised in an educational environment in which she had direct exposure to the influence of Masonic, Rosicrucian, and Baconian concepts. One of these concepts involves the labyrinthine aspect of the House’s design. The ancient mystery schools emphasized the tradition of the initiate. The novice student, called the initiate or candidate, was required to undergo a series of tests in order to prove that he was ready and worthy to advance to successively higher levels of learning. These levels are called Degrees.

In ancient times, the initiate was subjected to a test called the labyrinth. The labyrinth was usually an underground or enclosed maze-like structure consisting of dark, winding stairs and passageways. The initiate had to successfully find the correct path through the labyrinth’s numerous pitfalls, obstacles and traps. The purpose of the test was to force the initiate to develop and hone his powers of intuition and insight.

Although Sarah’s labyrinthine House serves the same function as the ancient prototypes, her labyrinth is more a symbolic introductory step into her puzzle. The greatest test for the initiate lies in his ability to understand and identify Mrs. Winchester’s remarkable mix of symbols and numbered code. Sarah’s love of Geometry and specific symmetric numbers is prominently displayed throughout the House. But most importantly, as we shall see, Sarah adopted the numeric, cryptographic techniques of Francis Bacon, incorporating them into her architecture along with specific Baconian symbols. Let’s examine them.

One of Francis Bacon’s many achievements in the field of encryption are his various cipher techniques. In fact, his “Bi-lateral Cipher” was so effective it became the model for modern day Morse code and computer operating systems.

As we have seen, Bacon infused coded cipher messages in all of his works, including the Shakespearean plays and sonnets, and his translated work known as the King James Bible. As earlier noted, most of Bacon’s ciphers involved the use of numerological and gematria tables. Such tables matched the twenty four letters of the Elizabethan-Jacobean Alphabet with specific numbers. The codes used by Bacon were generally a mixture of five different tables: Simple Cipher, Kaye Cipher, Reverse Cipher, Short Cipher and the Pythagorean Cipher.

Later, when the English Alphabet expanded to twenty six letters, the Pythagorean (1 through 9) Table became the paradigm used by modern numerologists. Sarah Pardee adopted all of Bacon’s encryption Tables—however, the 1 through 9 Pythagorean Table was her primary cipher of choice.

The Pythagorean 1 – 9 Table

Using the Pythagorean Table is a simple matter of matching the letters in a name or word with their corresponding numbers, then adding the numbers together until you have one, simplified number. For Example, the name Sarah = 20, which then simplifies to 2 because zeros are regarded as nulls (and are not counted). Pardee = 31 = 4. Thus, Sarah Pardee = 6. Sarah’s full name, however, was Sarah Lockwood Pardee. So, her middle name, Lockwood adds up to 25, which then simplifies to 7. And, 7 + 6 = 13, then, 13 simplifies to 4 (i.e., 1 + 3 = 4).

Francis Bacon didn’t adhere to the strict application of the “simplification rule.” As we have seen in earlier chapters the name Bacon, in Simple Cipher, adds up to the number 33. For personal and mathematical reasons, he elected to have that number represent his last name rather than the number 6. Likewise, the name Bacon, in accordance with the Kaye Cipher Table, adds up to the number 111. As we have seen, this became the second code number he used to represent his last name.

For reasons I will soon make clear, we know with certainty that young Sarah followed Bacon’s example. In fact, the plot grows thicker when we note that the names Sarah Pardee and Francis Bacon both correspond (in the Pythagorean Cipher) with the number 51. Moreover, when she included her middle initial (L), the numbers in Sarah’s name then added up to 54 which, when reversed (i.e. 45), corresponds to the name Shakespeare.

When Sarah first met William Wirt Winchester, she would have found his numbers to be nothing short of miraculous. First, his name adds up (in the Pythagorean Cipher) to the number 111 (just like Bacon in the Kaye Cipher). And, second, when each of William’s names are simplified, they become 777, i.e. William = 34, Wirt = 25, Winchester = 52.

As earlier noted, the number 777 is extremely important to Kabbalists, Rosicrucians and Freemasons. Moreover, William’s full name amounts to 21 letters. 21 consists of three 7’s—and, as we shall see, this is a consistent theme with all of the names in the Winchester family. Furthermore, the initials W.W.W. equate to 555, another crucial Kabbalistic-Masonic number.

Many married couples like to say their union is the product of some kind of ineffable destiny. Sarah and William’s destiny was not ineffable. Notwithstanding their mutual love, their union was destined by numbers.

Sarah Pardee Winchester, age unknown. Courtesy of the History Museums of San Jose

Upon her marriage to William, Sarah’s numbers reached a higher level of completion. As with Francis Bacon, Sarah realized that “numerical synchronicity” embodies the deepest underlying dynamic of destiny. Thus, the number 51 (Sarah Pardee) mating with the number 52 ( Winchester) combined in the most “unifying” of numbers, 103, i.e. 13.

William Wirt Winchester, age unknown. Courtesy of the History Museums of San Jose

The birth of the Winchester’s daughter, Anne Pardee Winchester (in 1866) resulted in a new set of numbers for Sarah to deal with. Mrs. Winchester carefully selected two primary numbers to represent her daughter’s name, i.e. 11, and 77. As we shall see, Sarah’s preference for the names Annie Pardee (56), and Annie Winchester (77) were important because they demonstrated a numerical kinship between Annie and Sarah, and Annie and William. For example, the name’s Sarah Pardee and Annie Pardee both consist of 5 letters followed by 6 letters for a total of 11 letters. Moreover, the name Annie Pardee corresponds with the number 56 in the Pythagorean Cipher. In a different way, each of the names William (34) Winchester (52) and Annie (25) Winchester (52) when simplified, equate to the number 77. However, the name Annie Winchester (simplified or not) still corresponds with the number 77 (Pythagorean Cipher). Furthermore, the names Sarah Pardee Winchester, William Wirt Winchester and Annie Pardee Winchester each consist of 21 letters. And as we have previously seen, 21 consists of three 7’s, or 777.

The reason we know that Sarah adopted Bacon’s numerological methodology stands on the concrete evidence she left behind as testimony to her thoughts and intentions. For example, it is certain that Sarah regarded 52 as the code number representing the name Winchester as evidenced by the 52 skylights in her House—and the fact that her earthly remains, along with those of William and Annie are interred in plot number 52 of New Haven’s Evergreen Cemetery. And just to insure we would understand that the connection between the number 52 and the name Winchester are not accidental Sarah deliberately placed coded inscriptions on the three tombstones of the Winchester family plot. They read: “BABY ANNE,” “SLW,” and “WWW.” These three inscriptions add up in the Pythagorean Cipher to 52. Furthermore, in addition to the number 111, Sarah adopted the Kabbalistic number 777 as a code number representing the name William Wirt Winchester—we know this because, in the decade following William’s death, she maintained precisely 777 shares of stock in the Winchester Repeating Arms Company. These are not coincidences—and we know what these and other numbers meant to Sarah.

As already noted, Sarah was weaving her tapestry of numbers long before she began the construction of her house. Her connection with Francis Bacon is undeniable. As we shall further see, Sarah had every reason to identify with Bacon, philosophically, artistically and spiritually.

We further note that virtually all of Bacon’s work was encoded as a multi-layered puzzle for later generations of “enlightened” individuals to discover. His work within his Rosicrucian circle, during the writing of the Fama Fraternitatus (the first of Bacon’s three Rosicrucian manifestos), reflects his use of the code name “F. B. Architect.” And, indeed, Bacon saw himself (at least metaphorically) as an architect. The architect theme shows up in virtually everything he produced. It is his foundation for what would later become Speculative Freemasonry, and, as we have seen, it is ubiquitous throughout his Shakespearean work.

The architecture as art legacy was first passed down by the Roman architect and philosopher Marcus Vitruvius Pollio. It was Vitruvius who first expounded the virtue of the mathematical value of Phi (the Divine Proportion, Golden Ratio, etc.). He held that architecture was the noblest and most perfect of all the art forms. The sacred knowledge of architecture was bequeathed only to the “initiate” who had proven to be “worthy.” Later, in the thirteenth century, the Italian mathematician, Leonardo Fibonacci translated Phi into real numbers. This rational system of numbers is known as the Fibonacci sequence. The arcane knowledge of Phi, and its relationship to architecture was adopted and guarded by the Knights Templar, only to go underground after their downfall in 1307, remerging as the “ Invisible College” of the Rosicrucian movement.

In their book “The Templar Revelation,” authors Lynn Picknett and Clive Prince point out the rather obscure fact that “the Rosicrucian movement was the cause of the Renaissance.” This was the Golden Age of Genius—and, of all the geniuses the Renaissance spawned, no one was more influential or as productive as Francis Bacon. As we have seen, he was the mastermind who single-handedly sired the English Renaissance and the Age of Enlightenment that would follow. Moreover, it was Bacon who gave the Rosicrucian movement its name and articulated its purpose. And as we have seen he created a new branch of the Rosicrucian Order called “Speculative Freemasonry.”

Bacon’s new, revolutionary innovations in the arts and sciences were built on the solid foundation of the “ancient wisdom.” As with the Templars, such knowledge was to be preserved and propagated through the tradition of the “initiate.”

Bacon’s philosophy further maintained the fundamental tenets of the ancient mystery schools, i.e. architecture as art, higher dimensional unification, and, most important, the theme of “concealment.” Bacon’s concept of concealment originated with his view of Proverbs 25 (in the Old Testament): “It is the Glory of God to conceal a thing: but the honour of kings is to search out a matter.” This is the underlying principle that evolved into both the “modern scientific method” and the Masonic Hiramic legend. Moreover, Bacon applied the theme of concealment to everything he touched—including his own life (the same was equally true of Sarah Winchester).

Sarah’s Puzzle

Francis Bacon and Sarah Winchester both understood that the only way to reveal all that nature conceals is through the transcendental science of numbers.

Therefore, following her loss of Annie and William, Sarah began to write not with words (as Bacon had), but truer to the Vitruvian tradition she chose speak to us in the pure language of numbers and architecture over a backdrop of concealment.

Like Rosslyn Chapel, the Winchester House serve’s as a higher dimensional puzzle. In order to discover its underlying meaning, one must follow the path of the initiate. To that end Sarah carefully crafted Masonic and Rosicrucian features into the structure of her labyrinthine House. Her concept of initiation closely parallels the Masonic and Rosicrucian method of subjecting the initiate to a series of progressive steps or Degrees in which he is forced to develop his powers of intuition and insight.

At the outset of each Masonic Degree the initiate (Candidate) expresses his wish to receive Light. With that in mind, let us begin the initiate’s journey down the path that Sarah laid out.

For a start, the front of the House, like Solomon’s Temple, faces true east. This is symbolically important as the east represents the source of Light (Knowledge and Wisdom). Moreover, like a Masonic lodge the House is emblematic of Solomon’s Temple. Mrs. Winchester regarded everyone who stepped onto her property as a prospective initiate. So naturally the initiate’s journey begins at the front wrought iron gates. Each gate is decorated with the Sun symbol (with 16 radiants). This symbol was used by Bacon in many of his engravings. The only difference with Sarah’s Sun symbols is that, instead of the usual face in the center, Sarah has inserted the image of an eight petaled daisy (more about the eight petals later).

Sarah’s special design for the insignia of the Senior Deacon of a Masonic Blue Lodge

The significance of the 16 radiants is multi-layered. But the primary importance here is that the pair of 16’s (standing side-by-side) is a reference to the calendar year 1616. This was, perhaps the most pivotal year in Bacon’s life. It marked both the death of his front man Will Shaksper, and the birth of his new, secret society of Speculative Freemasonry—and this was the year in which Bacon wrote and published his third and final Rosicrucian Manifesto The Chymical Wedding of Christian Rosenkreutz. Secondly, the number 16 simplifies to 7—thus, leaving us with a pair of 7’s. As we shall see in Sarah’s Ballroom, sevens are displayed in a more profound way.

Sarah’s insertion of daisies in the center of the two Sun symbols on the front, wrought iron gates are important because the daisy represents the two essential qualities of the initiate: Innocence and Fidelity. Moreover, the Sun symbol is the insignia of the Senior Deacon of a Masonic Lodge. It is the Senior Deacon who acts as the initiate’s guide throughout his initiation in all three of the Blue Lodge Degrees. By passing through Sarah’s gates, the initiate becomes his own guide and pursues the path of “Self Initiation.”

Once inside the gates, looking straight ahead, we view the front of the House through the frame of two palm trees that represent the twin porch pillars known as Boaz and Jachin at the entrance of Solomon’s Temple. For all Masonic initiates (Candidates), these are the first features they will pass through when entering the Lodge room.

View of the House from the front gate

After passing through the pillars the initiate then symbolically ascends a “Winding Staircase” leading into the Temple. Instead of allowing admittance in the front of her House, Mrs. Winchester required people to enter from the rear, through one entrance strategically located near the northwest corner. Her reason for this has to do with the fact that all Masonic initiates must enter the Lodge room through its northwest corner.

The entrance referred to by the tour guides as the “Switchback Staircase” (or the “goofy”) is built so as to wind from the center, outward, round and round, in the shape of an Archimedes Spiral until it reaches the second floor.

Middle Section of Jacob’s Ladder

It has 44 tiny steps. Each step is just under 2 inches in height. Thus, the effect is more like walking up a ramp than climbing a set of stairs.

Additionally, the staircase has 7 turns. Here, Sarah has ingeniously blended the symbolism of the “Winding Staircase” of the 2nd Masonic Degree with the symbolism of “Jacob’s Ladder.” According to the Kabbalistic and Masonic traditions, Jacob’s Ladder is a ramp that winds around 7 turns, ascending up into Heaven. Moreover, each of the 7 turns represents a progressively higher “degree” of enlightenment. Also, the 7 turns symbolize the 7 liberal arts and sciences as explained to the initiate in the “Winding Staircase Lecture” of the 2nd Masonic Degree.

The most crucial room in which Sarah wants the initiate to begin his journey of discovery is the “Ballroom.” This is the only room in the House which was constructed almost entirely without nails—an important feature that mimics the building of Solomon’s Temple. Entering the Ballroom, we notice a beautiful parquet floor with light and dark squares bearing a striking resemblance to the “checkered mosaic” floors of Masonic lodge rooms.

The Ballroom

Stepping further into the room, we have no choice but notice the obvious “Elephants” Sarah uses to capture our attention—these are two, elongated, stained glass windows which flank both sides of the room’s fireplace.

The Shakespearean Windows. Courtesy of the Winchester Mystery House

The two stained glass windows incorporate designs that were used by Francis Bacon—including his familiar winding banner. With the exception of the inscriptions written on the banners, the windows are exact mirror images of each other. Knowing the occidental mind reads from left to right, Sarah wants the initiate to start with the left window.

The inscription on the banner reads:

WIDE.UNCLASP

THE.TABLES.OF.

THEIR.THOUGHTS.

This line is from Act 4, Scene 5 of the Shakespearean play Troilus and Cressida. It should not surprise us that Sarah chose to start the initiate’s journey of discovery with words from this particular play. Clearly, Sarah was aware of Bacon’s placement of the name Winchester as the 20th word from the play’s end. It would be naïve to think she didn’t see the precise match with her name, i.e. 20 = Sarah (Pythagorean Cipher). As we shall see, Sarah provided numerous coded messages to confirm her connection with Bacon. The inscription on the banner in the right window reads:

THESE.SAME.

THOUGHTS.PEOPLE

THIS.LITTLE.WORLD

This line is from Act 5, Scene 5 of the Shakespearean play Richard II. The expanded text from which these words appear reads:

My brain I’ll prove the female to my soul,

My soul the father: and these two beget

A generation of still-breeding thoughts,

And these same thoughts people this little

world,

In humours like the people of this world,

For no thought is contented. The better sort,—

As thoughts of things divine,—are intermix’d.

This passage is an eloquent summation of Bacon’s theosophical outlook on reincarnation. Again, we should not be surprised that Sarah introduces us to her puzzle by demonstrating her view of her relationship to Bacon. Not only did she identify with him, but, in all probability, saw herself as Bacon reincarnate—as we shall see, Sarah manifests this view by incorporating the “Winchester Goose” as a numbered, coded message in the two windows.

The typical reaction people have when they first look at these inscriptions, is that they don’t seem to make sense. Along with Sarah’s inclusion of one of Bacon’s code devises called “stops” (i.e. periods or decimals), the words and manner in which they are arranged have the appearance of incompleteness—they seem to be out of whack. This is precisely the effect Sarah wanted the inscriptions to have on us.

Sarah knew that most people would simply shrug their shoulders and walk away. Moreover, she also knew this would be the initiate’s first “trial” or “moment of truth.” So, we are compelled to either walk away, or stand back and take a truly hard look at the matter. We are actually dealing with a choice between two options: one, either Mrs. Winchester was crazy, or two, she is cleverly guiding us toward an understanding of the methodology she employs for the sole purpose of solving her puzzle. For those who would choose the first option, go ahead and walk away—many other people have already preceded you!

However, once you conclude that Sarah was sane, and you opt to go with door number two, you are compelled to see that there is a rational purpose behind all of these seemingly insane features built into the structure of the House. Moreover, you must then conclude that these Shakespearean Windows function as the introductory step of Mrs. Winchester’s elaborate puzzle and she is inviting you (the initiate) to actively (not passively) participate in solving the puzzle. However, the revelations and insights to be gained through the initiatic process must be earned.

Like all of the other anomalous features we find in the House, Sarah wanted the display of apparent irregularity in the Shakespearean Windows to utterly shock our sensibilities. Clearly, what we see before us wasn’t placed there for Sarah’s self amusement. These windows were meant for other people! And, they aren’t just talking to us—they’re SCREAMING at us! Sarah has left instructions. She wants us to know and understand certain things. She has gone to great pains to leave a trail of clues that will lead us to the truth. All we have to do is pay close attention and follow those clues.

On a superficial level, the inscription on the left is Sarah’s way of saying “Open Sesame” to our minds—and, “Welcome to my puzzle.” The inscription in the right window is Sarah’s way of saying “Once you solve my puzzle, pass the truth on to others.”

Notice that, in choosing to use these two particular lines, she is accomplishing several things on different and deeper levels. First, Sarah wants us to achieve a better understanding of her by comparing her with Cressida and Richard II.

With regard to Cressida, most people presume that Sarah is alluding to the young maiden’s “flirtatious nature.” In fact, the traditional, orthodox, scholastic view of Cressida is that she is a “whore.” But this is not the point that Bacon (writing as Shakespeare) is trying to make, nor is it the point Sarah is trying to make. The deeper truth about Cressida is that she does whatever she must in order to survive—and Sarah, in her own way, saw herself as a survivor.

As to Richard II, Sarah identifies with the irony of Richard as an imprisoned, lonely king. However, both Richard and Sarah resolve to overcome their plight with the phrase: “Yet, I’ll hammer’t out.” For Richard, this is meant figuratively, but for Sarah, the interpretation took on a more literal meaning.

Now that we’ve had at look at the superficial significance of the Shakespearean windows, let’s analyze the matter more deeply. Clearly, Mrs. Winchester isn’t whimsically playing around with these particular passages from Shakespeare. As with all things in the House, there is more, here, than meets the eye. Like Bacon, Sarah’s use of numbers always leads us to a deeper core of meaning.

The careful selection of these lines from Act 4, Scene 5 (Troilus and Cressida), and Act 5, Scene 5 (Richard II) reaches beyond Sarah’s love of synchronicity. Borrowing from Bacon’s methodology, she is purposefully showing us the numbers 45 and 55. We remember that the number 45, with regard to the Pythagorean Cipher, corresponds to the name Shakespeare. Additionally, the number 55 (Pythagorean Cipher) matches the name Hiram Abiff. When we combine the number 45 (Shakespeare) with the number 55 (Hiram Abiff) the result is 100 which is Simple Cipher for the name FRANCIS BACON. In one brilliant stroke, Sarah’s code reveals Shakespeare, Hiram Abiff and Francis Bacon to be one and the same person. This is critical to understanding both Sarah’s motivation and thinking.

Furthermore, with regard to the two Shakespearean inscriptions, Sarah has deliberately omitted the first word in each 8 word line so as to leave only 7 words in each line. As we saw with the front wrought iron gates, we are again left with two 7’s. Unquestionably, she is talking to us in a numbered code. Like Bacon, Sarah uses encryption code to guide us to higher levels of insight. We are forced to ask if Sarah wants us to view these as two, separate 7’s or as the number 77 ?

Also, when we take a closer look at the words UNCLASP and TABLES, we realize that in Bacon’s time the only things to be unclasped were books—secret books—books containing Encryption Codes with an Encryption Table to decipher such codes. In fact, some of Bacon’s engravings show him holding books with CLASPS. But then, where are we to find such a book? And Tables? Where is the Encryption Table?

Naturally, Sarah knew that we would eventually look up at the magnificent ceiling of her “Ballroom.” With the exception of the decorative middle panel that supports the 13 globe chandelier, we observe 9 main panels. Because we are already familiar with Numerological Tables, we know that in displaying the numbers 1 through 9, Sarah is alluding to the Pythagorean Table. However, she has ingeniously raised the bar by including 13 sub panels with each of the 9 main panels. But, she has done something unexpected. In showing us 9 sets of the number 13, she has forced us to multiply. In fact, she has already done it for us. Sure enough, 9 x 13 = 117 (Bacon’s code number for John Dee). Moreover, we have the numbers 11 and 7 standing side-by-side. Thus, Sarah induces us to multiply 11 x 7. Going back to the windows we now have the answer to our original question. We are to view the two 7’s as the number 77. Moreover, when we consult the Pythagorean Table, we realize that the number 77 corresponds both to the words “ Winchester goose” and the name Annie Winchester.

In one simple lesson, Sarah has skillfully introduced the initiate to the rudiments of her number system. Moreover, she has employed a brilliant device in the Shakespearean Windows to drive home the connection between Shakespeare, Hiram Abiff, Francis Bacon and herself. Upon closer examination of the “Windows,” we notice that each has three partitions.

Thus, we have the number 3 in both windows, rendering Bacon’s number 33. Furthermore, Sarah’s use of Bacon’s “stops” (decimals or periods) in the inscriptions indicates that something is further concealed in code.

With the exception of the inscriptions on the banners, the symbolic images in the left and right windows are exact mirrors of each other (similar to Bacon’s headpieces). In fact, the various symbols are distinctly Baconian.

In the center of each window we see the Glass of Bacon’s muse, the goddess Pallas Athena. And, we recall that her Glass (mirror) reflects the light of knowledge and wisdom.

Elsewhere in the windows we see numerous “crooked staffs” connected to each other like branches growing out of Athena’s mythical olive tree. These staff-like branches with their distinct hooks are a direct allusion to Pan’s crooked staff that is also brandished (like Athena’s spear) against the serpent of ignorance. We are also reminded of the image of Francis Bacon (in Whitney’s Book of Emblems) stamping at the serpent with a similar staff. A close scrutiny of the bottom portion of the Shakespearean Windows reveals the crooked staff entangled in a serpent-like creature. Additionally, Sarah cleverly provides subtle hints of Pan’s presence as we detect glimpses of his horns blending in with the Window’s overall design.

Sarah’s use of Pallas Athena’s Glass and Pan’s crooked staff indicate that something more is concealed in the design of the Shakespearean Windows. Furthermore, she is alluding to Bacon’s underlying philosophical premise as given in Proverb 25, i.e. “it is the glory of God to conceal a thing and the glory of kings to find out a thing.” As a matter of fact, on page 45 of his personal copy of The Advancement and Proficience of Learning (currently residing in the British Museum), Bacon penned a drawing of Pan’s crooked staff in the margin next to the book’s text regarding Proverb 25—and just beneath the drawing, he has written the words “Hide and Seek.”

Adding further to the hide and seek theme, Sarah has introduced another tantalizing element to the Windows’ design. We notice that a tiny ball is tightly tucked into the crook of each of Pan’s staves. Sarah has intentionally shaded each ball so as to give it a three dimensional effect. We can clearly see that this is a ball-like feature, and not a circle. This symbol should be partially recognizable to the Master Freemason, but something is missing.

We haven’t forgotten the “Baconian stops” Sarah has incorporated in the Shakespearean inscriptions. However these stops are shaped like small arrowheads pointing to the partitions above. Sarah is exhorting us to rearrange the order of the partitions. Using photographs of the two Shakespearean Windows, we cut them into thirds, resulting in facsimiles of the six window panes. We then move them around like pieces of a jig-saw puzzle. When they are properly realigned, a stunning, new pattern emerges. Using Bacon’s “Letter C” figure in his “double A” design, Sarah has created an ingenious way to show us another word or name that is important to all Master Masons. It is a name from the Old Testament, “Tubal-Cain.”

As noted earlier, John Dee’s secret signature was an elongated number 7 with two circles under it, representing his 007 identity. This became the basis for a hieroglyphical pun in the form of a cane flanked by two balls representing Tubal-Cain. Throughout the centuries, the Tubal-Cain symbol has employed either a cane shaped like a backward number 7, or a cane with a simple crooked handle. Naturally, Sarah is making use the latter form.

John Dee’s 007 signature as Tubal-Cain, and the traditional Tubal-Cain symbol.

The top and bottom panes properly rearranged showing Sarah’s Tubal-Cain Symbols

Historically, the Tubal-Cain symbol has generated controversy because of its phallic connotation. It is highly probable that Mrs. Winchester found the symbol too risqué for her use—thus, she devised a new symbol representing Tubal-Cain in the form of the Letter C with two balls. With the proper realignment of the six window panes, we now have three letter C’s, two of which have a ball tucked under the top and bottom horns of the letter’s arc. The solitary letter C, of course, is the Roman Numeral 100 representing the name Francis Bacon (Simple Cipher). And, as we have seen, the two letter C’s facing each other give us the number 33 (Bacon in Simple Cipher).

Another significant symbol associated with the Master Mason that materializes with the proper realignment of the six panes of the Shakespearean Windows is the Hourglass. In both the Rosicrucian and Masonic traditions, the Hourglass is “emblematic of human life.” Furthermore, the realignment of these two panes gives us the words “THE TABLES OF THOUGHTS PEOPLE.” It is no coincidence that these particular words, thus rearranged, now add up (in the Pythagorean Cipher) to the number 111.

Properly aligned Center Window Panes showing the Hourglass

There are other places in the House where the initiate will learn more lessons. For example, on the second floor, near the front of the House, there is a gallery of beveled, stained glass windows featuring the fleur-de-lis design associated with both the Prince of Wales and the House of Tudor. Moreover, Sarah has added a novel twist to her Tubal-Cain devise by joining two of them in such a way as to form the number 3. Thus, she has one (Tubal-Cain) number 3 displayed in the right border of the windows, and a second (reversed) number 3 shown in the left borders—rendering the number 33 with the fleur- de-lis pattern occupying the middle portion of each window. It is a virtual shrine to Bacon.

Bacon fleur-de-lis windows with left and right number 3’s facing each other

Bacon’s “Double A” Headpiece with fleur-de-lis design, and the letters C facing each other

Not far from the Bacon-fleur-de-lis windows, Sarah exhibits the most ornate stained glass window in the entire House. It is prominently displayed at the top of a 13 step staircase. It was manufactured in accordance with Sarah’s specifications by the famous Tiffany Glass Company at a cost of approximately $1,500. To make matters more interesting, Sarah has the window facing north with no perceivable source of light. An important part of the puzzle goes back to Rosicrucian beginnings in ancient Egypt . The Egyptians saw the path to heaven as a 12 step staircase with a magnificent door at the top. The gate to heaven would truly be the most splendid of all. Although the 12 steps were sufficient to bring one up to the heavenly door, they were insufficient to deliver one into heaven. The riddle lay with the worthy ascendant realizing that there is an invisible 13th step that could only be crossed once the door had been opened for him by a divine source from within. The reason for the north facing orientation of the window is that it leads to the “immortal star” Sirius. To the ancient Egyptian mind, this is where heaven is located.

It should also be noted that Solomon’s Temple had a magnificent “Great Golden Window” that faced north.

The most obvious Baconian devices in the Tiffany Window are Sarah’s Tubal-Cain symbols. But Sarah has introduced another clever design in the form of winding ribbons located in the upper center that take the shape of the letters W (at the top) and S (just beneath). Notice how they mirror each other. The letters W S stand for William Shakespeare, and Winding Stairs, while the letters S W represent Sarah Winchester. Notice that the letter W is equivalent to the number 5 (Pythagorean Cipher), and the letter S is equivalent is the number 1—hence, 51. In accordance with the Pythagorean Cipher, we recall that the number 51 corresponds to both the names Francis Bacon and Sarah Pardee. Moreover, with regard to the name William Shakespeare, there are 7 letters in William, and 11 letters in Shakespeare—hence, 711—hence, 72, Sarah (20) Winchester (52).

The Winchester Tiffany Window. Courtesy of the Winchester Mystery House

Sarah’s bedroom is located on the south side of the second story. The ceiling is a perfectly square grid consisting of 49 (7 squared) individual squares reminiscent of a mathematical table devised by John Dee. When Sarah looked up at this grid, she saw an array of significant numbers. First, she saw the number 13, i.e. 4 + 9 = 13. Next, she observed 7 horizontal squares, 7 vertical squares and 7 diagonal squares, rendering the number 777. And, by simply multiplying 777 x 13, she produced the number 10101, or 111.

The bedroom’s south facing windows overlook a beautiful lawn and garden. In the middle of the lawn we see a magnificent crescent shaped hedge, accentuated with brilliant, yellow chrysanthemums.

The Crescent Hedge as seen from Sarah’s bedroom window
Courtesy of the Winchester Mystery House

The significance of this unusual feature has to do first, with Sarah paying homage to Francis Bacon, for the crescent moon, as we are about to see, is emblazoned like a brand on the side of the boar in the Bacon’s coat of arms.

Francis Bacon’s Coat of Arms with crescent moon brand on the boar at the top

Because it is shaped like the Roman Numeral 100 (“Lunate Sigma”), Bacon used the crescent moon as another devise to represent his name—and we are reminded of Bacon’s words in Sonnet 111: “Thence comes it that my name receives a brand.”

Second, “The Crescent” was a periodical magazine of poetry and prose written, under various pseudonyms, by Sarah and her classmates, and published by her alma mater “The Young Ladies Collegiate Institute” of New Haven, CT. The artwork on the magazine’s cover featured a crescent moon in its waxing stage.

Front Cover of the Crescent. Courtesy of the Whitney Library, New Haven, CT.

Another important function of the crescent hedge is to emphasize the moon’s relationship to the number 13. It is the lunar number because there are always 13 full moons in a year. For this reason, the Mayans and the Chinese had 13 month calendars. To this day, the 13 month calendar is more accurate than the Gregorian.

Additionally, Sarah covered the walls of her bedroom with special wallpaper displaying the “Triquetra” symbol. According to Celtic tradition the Triquetra represents the three lunar goddesses who, in turn, represent the three phases of the moon.

One of many Triquetra symbols embedded in the wallpaper of Sarah’s bedroom

Knights Templar Cross with Triquetra Symbols

Sarah also wants to underscore the relationship between the moon’s reflective light and the “Astral Light” AKA the Akashic record. Here, she is affirming her Theosophical point of view.

In the exact center of the House, we come upon the so called “séance room.” We remember that this, according to the folklore, is where Sarah supposedly conducted midnight séances for the purpose of receiving building instructions from the spirits. Such a notion, as any practicing Rosicrucian knows, is utterly absurd. All Rosicrucians have a room or space like this situated (as closely as possible) in the center of their homes. This serves the practical purpose of being far from the distraction of outside noise. The room is actually called the “Sanctum.” Freemasons refer to it as the “Chamber of Reflection.” The Sanctum is where Rosicrucians study, meditate and perform private ritual.

Sarah’s Sanctum is shaped like a cube, emulating the Sanctum Sanctorum, or Holy of Holies of Solomon’s Temple. The room measures 11 ft. x 11 ft. x 11 ft. The dimensions are not accidental. Sarah uses the 11, 11, 11 cube for several reasons. First, like Bacon’s play on the letters L, L, L in Love’s Labours Lost—11, 11, 11 combined, becomes the number 33. Second, 11 x 11 x 11 renders the (Ramanujan) palindromic number 1331. Notice the Masonic metaphor of the number 33 enclosed within the number 11, as it is flanked by the twin, Masonic pillars, i.e. 1 33 1. Also, 13 and 31 possess the unique quality of generating (reverse) palindromic twins when they are squared, i.e. 13 squared = 169, and 31 squared = 961. Finally, Sarah’s use of the number 11 illustrates the simplicity of the cube’s symmetry. The simplest mathematical expression of cubical symmetry is 111111, which Sarah hoped we would discover by simply multiplying the number 11 x 777 x 13.

Originally, Sarah’s Sanctum Sanctorum was painted entirely blue. This is important because it mimics the Masonic concept of the “Canopy of Heaven” or “Heavenly Arch” which is widely featured as part of the décor in Masonic Lodge-rooms. Finally, Sarah had 13 pegs installed in one of the Sanctum’s walls. Each peg held a different colored robe, consistent with the Rosicrucian practice of wearing a different colored robe for each lunar month.

On the ground floor, not far from Jacob’s Ladder, there is an unfinished room which Sarah planned to use as a second “Ballroom.” Upon entering the room we notice a rough, horizontal cross-beam extending across the upper portion of the south wall. To the untrained eye, the beam has the appearance of just another piece of wood. However, any astute Freemason will recognize its remarkable resemblance to the “24 inch gauge” of the Masonic 1st Degree. But this facsimile of the 24 inch gauge is made to scale, spanning a length of approximately 16 ft. Moreover, the darkly stained beam has 46 lightly colored vertical rule lines which divide the gauge into 47 evenly spaced segments. Sarah clearly uses this device to exemplify Bacon’s coded message in Psalm 46 of the King James Bible.

The number 46 (i.e. 406) represents Christian Rosenkreutz (Kaye Cipher), and the number 47 refers both to the Master Mason (i.e. the 47th proposition of Euclid’s Elements known as the Pythagorean Theorem) and to the name Hiram (Simple Cipher). We further recall how Bacon designed the text so that the word “shake,” the 46th word from the beginning of the Psalm is connected to the word “spear,” the 47th word from the Psalm’s end, by exactly 111 words. Moreover, when we place the numbers side-by-side, i.e. 4746, then, reverse their order in accordance with the Kabbalist “Atbash Cipher,” i.e. 6447, then combine 64 and 47, the result is 111.

In another part of the House, the initiate comes to a landing connecting two staircases, each leading to different second story rooms. The staircase to the left has 7 stairs while the one on the right has 11 stairs. This feature is referred to as the “7/11 staircase.” Notice how 711 is the reverse of the 117 displayed in the Ballroom ceiling—and, as we have seen, Sarah also saw it as another way to express her name as 711 simplifies to the number 72, corresponding to Sarah (20) Winchester (52) in the Pythagorean Cipher. Additionally, we are reminded that the name William Shakespeare renders the numbers 7/11 as there are 7 letters in William, and 11 letters in Shakespeare.

Another important aspect of the 7/11 staircase is that it forms a large Letter Y, which symbolizes the “fork in the road.” The initiate must make a choice between traveling the easier left path or climb the more difficult right path. Naturally, the right path is the correct one. If a man were to traverse these stairs from the second floor, left to right, he would be traveling from west to east. In all Masonic lodges, one is always regarded to be traveling from west toward the source of light in the east.

Furthermore, Sarah adds a lesson in “higher dimensional mathematics.” When a man walks down 7 steps, and then up 11 steps, what has he gained? The obvious answer is 4. But in higher dimensional mathematics, the number 4 can translate or rotate into multiple variations of itself, i.e. 13, 31, 22, 112, 211, or 1111. As we shall see, there is a unique relationship between the numbers 7, 11, and 13. Thus, in a world governed by higher dimensional dynamics, the difference between 7 and 11 is the “Fibonacci” prime number 13.

When I first walked the 7/11 staircase, and earned this insight about the number 13, I rushed back to the Ballroom. I knew that Sarah had concealed the number 13 in the middle, between the Shakespearean Windows, in a higher dimensional way. And, sure enough, there it was… where no one would normally think to look for it! The image in the mirror above the fireplace was a reflection of the room’s 13 globe chandelier. It was perfect! It was exactly as Sarah had planned it.

Higher Dimensional Geometry:

Why the Winchester House Seems So Mysterious

By the time Sarah Pardee was born, Francis Bacon’s modern scientific method had exploded into a virtual catalogue of new, revolutionary theories of the intricate workings of the universe. Bacon’s search for the grail of all grail’s, i.e. the “Theory of Everything” was well underway. Hans Christian Oersted’s discovery of the unification of electricity and magnetism (1820), along with Charles Darwin’s Theory of Evolution (1838) had stirred the new, scientific caldron to such an extent that natural forces were being explained as a dynamic evolving phenomenon rather than a static, passive entity.

No one had understood the underlying dynamics of the universe better than Francis Bacon who viewed nature as a model of the universe based on a set of fundamental rules and laws immanent from the outset in its ratio, order, structure, measure and corresponding symmetries. Thus, the “Theory of Everything” had (in the Baconian sense) become a quest for a “Grand Unified Theory” of all the forces of nature.

The curriculum of “The Young Ladies Collegiate Institute of New Haven” placed a heavy emphasis on scientific studies. Mrs. Winchester’s application of the latest technological innovations in her mansion, demonstrate both her scientific background and her passion for keeping up with new discoveries. Since she clearly regarded her House as a living puzzle and a work of architectural art, we are compelled to examine the environment that influenced her views and her work.

The scientific curricula that Sarah studied included Michael Faraday’s seminal work on electromagnetic fields, along with the scientific and mathematical works of William Thompson, Georg Bernhard Riemann, and William Rowan Hamilton. The most revolutionary scientific development of young Sarah’s time was the discovery that the forces of nature are a product of “higher dimensional dynamics” of the geometry of space. As we shall see, the anomalous features throughout Mrs. Winchester’s mansion are a testament to the profound impact “higher dimensional geometry” had on its design.

The Riemannian Revolution

German mathematician Georg Bernhard Reimann (1826-1866) realized that the forces of nature might be nothing more than a manifestation of the geometry of space. He reasoned that forces might be best explained in terms of warps in a higher dimension. If space could tell mass how to move, mass would, in turn, have its affect on space. Moreover, Riemann realized that all space transcends the flat, two dimensional geometry of Euclid. Therefore, in describing the dynamics of space, a new, higher dimensional model was required. If warps in space were the cause of natural forces such as electromagnetism and gravity, the structure of space had to conform to a higher dimensional curvature. Thus, Riemann devised a new, higher dimensional geometry that demonstrates how parallel lines can intersect, and arcs, rather than straight lines, can be the shortest distance between two points. Moreover, Riemann’s new view predicted the existence of a forth spatial dimension.

The Riemannian revolution had a profound impact both on nineteenth century science and Sarah Winchester. A new, simplified view of the universe had opened up in which unseen forces, from the structure of atoms to the dynamics of gravity were becoming better understood from the perspective of higher dimensional space.

Riemannian geometry, along with the mathematical equations of William Thompson and William Rowan Hamilton conclusively demonstrated the existence of higher dimensions.

The concept of a forth dimension became an obsession that permeated both the scientific and academic communities of the latter nineteenth century. Artists and intellectuals began to express their views of how the dynamics of higher dimensional space might work.

An English mathematician by the name of Charles Dodgson, writing under the pseudonym Lewis Carroll, wrote a children’s book that described the mind boggling properties one would encounter in a forth spatial dimension. The book, of course, was Through the Looking Glass—a fitting title, considering the glass or mirror had been regarded as a portal to higher dimensions since Dee and Bacon’s time.

In Carroll’s “wonderland,” everything seemed to defy common sense. The distinction between large and small seemed to dissolve. Time could speed up, slow down or stand still. Through the Looking Glass had many of the qualities that would eventually be understood as the hallmarks of Einstein’s Theory of Relativity. Sarah seems to borrow from the pages of Lewis Carroll as she shows us large doors that lead into small space and small doors that open up into ridiculously large space.

Higher dimensions consist of a unique set of “super-mechanics” that transcend the limited, box-like structure of length, width, and height. To form an idea of what that would entail, try thinking in reverse. Try to imagine what living (and perceiving) in two dimensional space would be like. Everything would be completely flat. You would be unable to cross over a line. Three dimensional objects such as cubes, spheres and pyramids would seem impossible because our limited perception would only permit us to observe these objects as two dimensional squares, circles and triangles. And, if someone were to try to describe cubes, spheres and pyramids to us, we would tell them they were crazy. That’s what we’re dealing with when we try to imagine the properties of higher dimensional space.

The realm of higher dimensions is, in fact, a kind of “Super Space” where things that seem to defy common sense in three dimensions actually make complete sense from the perspective of higher dimensions. For example, when viewed from a higher dimensional perspective, a solid wall would seem more like a broken line. Not only would we be able to walk over it, we would also be able to walk through and around it in ways we otherwise wouldn’t imagine possible. Furthermore, distinguishing between large and small, up and down, front and back, left and right, inside and out, etc., would seem equally absurd to us. Thus, what appear to be upside-down pillars, chimneys and skylights that have overhead roofs, and doors or stairs that lead into solid walls make perfect sense when viewed from higher dimensions. Sarah Winchester was fully aware of Riemannian geometry when she incorporated higher dimensional properties into the architecture of her amazing puzzle.

Escher

Naturally, Sarah was in good company with regard to expressing the new view. Artists such as Georges Braque, and Pablo Picasso were painting stunning images depicting a forth dimensional world view appropriately called “cubism.” However, no one was more in step with Sarah Winchester’s perspective than the Dutch artist M.C. Escher. It is not known if Sarah and Escher ever met. However, their approach to higher dimensional expression is remarkably similar. It’s as if they were reading from the same book. They both made use of architectural devices and features that defy the conventions of ordinary three-dimensional space. In fact, Escher, like Sarah, shows us seemingly impossible stairs and pillars.

Relativity by M.C. Escher

Escher also saw the reflective images in mirrors as true representations of higher dimensional space. Escher wrote:

The spherical world cannot exist without the emptiness around it, not only

because ‘inside’ presumes ‘outside’ but also because in the ‘nothing’ lie the

strict, geometrically determined, immaterial middle points of arcs…There is

something in such laws that takes the breath away. They are not discoveries

or inventions of the human mind, but exist independently of us.

It is an interesting note that Escher felt a greater kinship with mathematicians than with other artists. Another crucial element Escher and Sarah Winchester shared was their understanding of the unifying nature of the mathematical symmetry which forms the basis for all higher dimensional structure.

The Escher-Penrose Triangle

The features Sarah and Escher show us are only glimpses of higher dimensional shadows. Since we haven’t yet evolved into beings capable of higher dimensional perception, we are forced to understand the dynamics of higher dimensions through the precise language of numbers.

We may well ask what value does higher dimensional mathematics have for us? The answer is that without higher dimensional mathematics, such as the mathematical innovations of William Rowan Hamilton or Sophus Lie, many of the technologies we take for granted from computers, cell phones, to landing robotic space craft on Mars, etc., wouldn’t be possible.

Bacon’s dream of unlocking all of nature’s secrets requires our understanding of the dynamics of higher dimensional mathematics. It sounds complicated, but it’s not. As Sarah and Escher saw, the beauty of higher dimensional numbers lies in their simplicity and “symmetry.” As we shall see, simplicity and symmetry are inter-related. It’s the stuff our universe is made of.

Sarah’s puzzle may ultimately help us discover the “Theory of Everything.” However, the final KEY to unlocking Sarah’s puzzle is in her numbers.

Winchester Numbers

As we’ve seen, the dynamic family of the prime numbers 7, 11, and 13 form the basis of Sarah’s system of numbers. No matter where we go, both in and around the House, Sarah has gone to great lengths to put her numbers on display. As a matter of practicality, I will hereafter refer to them as “ Winchester numbers.”

Throughout her lifetime, Sarah primarily saw 13 as her number. However, she also keyed on the “Master number” 11, as it applies to her name. This she did by counting the number of letters in her name, i.e. Sarah = 5, Pardee = 6. Hence, 5 and 6 combined = 11. Furthermore, she favored the name Annie Pardee for her daughter as evidenced by the manner in which she had Annie’s obituary printed: “ Winchester, ANNIE PARDEE.” The all Caps part of the name precisely matches the number of letters in the name Sarah Pardee. Moreover, the name Annie Pardee corresponds (Pythagorean Cipher) to the number 56. This is important as it reveals the close bond Sarah felt for her daughter.

One architectural device Sarah used to illustrate her view of the relationship between the numbers 11 and 56 is her arrangement of the decorative wooden posts that align the exterior railings of the two, third floor balconies above the front porch of the House. The posts alternate: one, right-side-up, one, up-side-down, one right-side-up, etc.—resulting in 5 right-side-up posts and 6 up-side-down posts.

Elsewhere about the House, Sarah throws other numbers into the mix, and we begin to see that Winchester numbers, although generally connected to family names, ultimately take on a much deeper meaning. For example, we recall that Sarah displays the number 49 (7 squared), along with the number 777 in her bedroom ceiling. Moreover, the House has 47 chimneys. We easily see the correlation to the names Anne Pardee (47 in the Pythagorean Cipher), and Hiram (47, Simple Cipher). Furthermore, it is also the number that is emblematic of the Masonic 3rd Degree as the newly “raised” Master Mason is twice informed that the number refers to the 47th Proposition of Euclid’s Elements, better known as the “Pythagorean Theorem.” And, just to make sure we understand that her display of that number isn’t accidental, Sarah repeated the number (according to the official, WMH literature) by building 47 staircases. Thus, Sarah emulates the dual allusion to the number 47 in the Masonic 3rd Degree lecture by displaying the number twice.

This, of course, isn’t the only instance in which Sarah has joined the numbers 4 and 7 together. As we saw with “Jacob’s Ladder,” she has combined 44 steps with 7 turns—resulting in the number 51, corresponding to the names Sarah Pardee and Francis Bacon (Pythagorean Cipher). But, the matter runs still deeper when we consider that, in showing the number twice, Sarah is also revealing a different perspective as 47 47 transforms (rotates) into 44 77—and, when these two numbers combine, we have the number 121 (11 squared) which then rotates (12 + 1 = 13) into the number 13.

Daisies, and the Number 13—the Key to Phi

As we saw with the wrought iron gates in front of the House, Sarah displays two, eight petaled daisies. In fact, Sarah shows us daisies everywhere, both in and around the House. They are carved into wood fixtures—they appear in most of the stained glass windows. And, many of the species of the daisy flower can be found flourishing in the extensive gardens about the House.

The daisy was special to Sarah for two essential reasons. First, it symbolizes the initiate. And, second, it is, unquestionably, one of nature’s finest examples of the “hidden” unifying symmetry of the number 13.

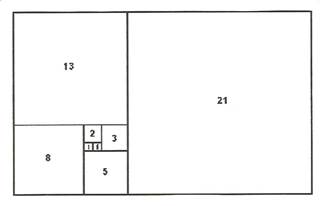
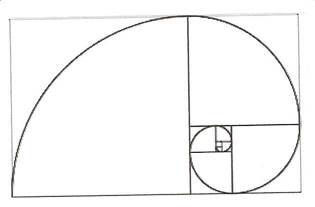
Many species of the daisy have 13 petals. Moreover, most daisy species have 13 branches growing out of their stalks (when they mature), and they possess another remarkable feature—the head of every daisy flower forms a “Fibonacci Spiral” consisting of 34 tiny florets spiraling clockwise, inward, from the outer ring to the center—and, 21 florets spiraling, outward, counter-clockwise from the center to the outer ring. The “invisible difference” is 13.

The value of Phi (the Divine Ratio, or Golden Mean), whose mathematical sequence was discovered by the mathematician Leonardo Fibonacci, was not invented by man. It is nature’s arbitrary template by which all natural structures, from atoms, flowers, trees, seashells and star galaxies comply with specific symmetric parameters. Such symmetry is governed by harmonics of “wave function” in which the growth of any given wave pattern flattens out when it reaches the 8th ordinal point in the Fibonacci sequence, which corresponds to the number 13. It’s an immutable law.

The “ordinal” numbers in the sequence are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ad infinitum. Note the number 13 occupies the eighth ordinal position in the sequence. Note further that the sequence is simply an endless repetition of combining a number with the preceding number in order to arrive at the next number in the sequence, e.g. 1 + 1 = 2, then 1 + 2 = 3, then 2 + 3 = 5, then 5 + 3 = 8, then 8 + 5 = 13, and so on.

Thus, 13 is the most coherent, unifying number in the Fibonacci series. From the beginning of civilization, the geometric value of Phi (and the number 13 in particular) has been used as the basis for all great architectural endeavors. To further elaborate on this point, authors Jea Yu and Russell Lockhart tell us:

In the Fibonacci series, it is at the eighth ordinal point that the ratio between

the series values become constant values. The eighth ordinal is the number 13.

Since this point is the point in the series at which there is no further change in the

growth constant, this would seem to be a reasonable basis for taking 13 periods as

the maximum number of periods by which a reference point and a structuring

point can be separated in order to constitute a “coherent” wave…There are other

approaches as well that arrive at the number 13 as defining the limit of a coherent

structure. The pyramids, for example, are built according to the “growth” of the

number 13. Stonehenge is built precisely on the spot where 13 describes the

hypotenuse of a triangle (the sides being 5 and 12) with the base at the Blue Stone

in Wales and at Lundy Island in the Bristol Channel. The point at the Channel’s

Calday Island divides the base 5 precisely into 2 and 3. The length of the

hypotenuse drawn from this point to Stonehenge is 12.368. This is exactly the

number of full moons in a solar year. It is extraordinary that Stone Age peoples

would be able to build such a sophisticated “clock” as Stonehenge is, and to locate

it at precisely 13 units from the Blue Stone origin in Wales . Astonishingly, the

continuation of this line crosses precisely at the location of the Great Pyramid at

Giza, which had not yet been constructed at the time of the completion of

Stonehenge.

Tiled Fibonacci Sequence

Fibonacci Spiral

As we are about to see, Sarah always displays 8 petaled daisies in pairs. Since there are no true species of the daisy family having as few as 8 petals, it is apparent that Sarah uses the 8 petaled daisy as a device to emphasize the Fibonacci relationship between the numbers 13 and 8.

13 therefore manifests the ultimate (invisible) boundary of all the coherent symmetries from which the structure of the universe is formed. It is literally the Key to Phi.

Quite remarkably, in theoretical physics, the leading candidates for the “Grand Unified Theory” AKA the “Theory of Everything” are “String Theory” and “M Theory,” which are both based on a simple equation involving a pair of 8’s, i.e. E (8) x E (8). The E stands for “Exceptional,” while the 8, of course, refers to the eighth ordinal point (occupied by the number 13) in the Fibonacci sequence. As we have seen, what makes E (8) exceptional is that it defines nature’s maximum limit for symmetric growth. Without symmetry, the universe and everything in it would not be coherent—rather it would be chaotic.

In addition to being the Key to Phi, 13 is also the dominant unifier of the three, primary Winchester numbers (i.e. 7, 11, and 13). However, the synergistic application of all three numbers (or their variants) is required in order to achieve the product of their higher dimensional symmetry. And, as we have seen, higher dimensional dynamics involve simple multiplication.

The evidence shows that Sarah made use of an algorithmic system in which her trio of symmetric prime numbers produce amazing results. For example, let’s multiply (get out your calculator) the numbers 7, 11, and 13 by any two digit number—let’s use the number 12. We multiply: 7 x 12 = 84. Then, 84 x 11 = 924. Then, 924 x 13 = 12012. Voila, one, dynamic level of the symmetry is revealed. Now, let’s go to a higher level using the 777 symmetric triplet. 777 x 12 = 9,324. Then, 9,324 x 13 = 121212. Let’s take it still higher by multiplying 12 by 7 squared (49). 12 x 49 = 588. Then, 588 x 121 (11 squared) = 71,148. Then, 169 (13 squared) x 71,148 = 12024012. Notice that, in the center, the value of 12 has doubled to 24.

Another remarkable symmetry occurs by simply multiplying: 11 x 777 = 8,547, then, 8,547 x 13 = 111111.

These stunning symmetries derived from the application of the dynamic trio of Winchester prime numbers reveals an underlying unified principle that indicates a transcendental, higher truth is at work. The late Cal Tech physicist Richard Feynman said “You can recognize truth by its beauty and simplicity…because the truth always turns out to be simpler than you thought.”

The Winchester Algorithm

As mentioned earlier, Mrs. Winchester undoubtedly discovered the dynamic trio of symmetric primes by studying Bacon’s use of them. Additionally, she studied the higher dimensional mathematics of William Thompson (Lord Kelvin), and William Rowan Hamilton.

Thompson (1824-1907) theorized the existence of “Vortex Atoms.” These are not atoms in the ordinary sense, but rather behave like tiny, sub-atomic “whirlpools,” resonating and stretching in various modes of symmetry in a vast higher dimensional foam or ether. What Thompson was describing (nearly one and a half centuries ago) was, essentially, the mechanics of what is now called “String Theory.” The fundamental problem with the Vortex Atom (as we now know) is that, theoretically, it functions as a “blob.” In order to be self-consistent, the blob would have to resonate at the speed of light—which we now know is an impossible feat for a blob-like structure to perform. However, it was later demonstrated that a string-like structure can resonate at the speed of light—hence, “String Theory” instead of “Blob Theory.”

The higher dimensional atomic theory of the latter part of the nineteenth century required a higher dimensional brand of mathematics to describe its functions. Thompson never fully achieved that end. However, the Irish mathematician William Rowan Hamilton formulated a system in which the symmetries governing wave function in four dimensional space can be revealed. He called his invention “Quaternions.”

The Winchester algorithm is a simplified variation of Quaternions, except it only uses real numbers (instead of Hamilton’s imaginary numbers). Moreover, two numbers are always multiplied by each other, leaving a product that is then partitioned, and the partitioned numbers are then added together resulting in a sum. For example, 52 x 88 = 4,576. This product can then be partitioned as 45 76, which, when combined becomes 121 (11 squared), or, it can be partitioned (from the inside-out) as 57 46, which, when combined equates to 103 (13). Or, it can be partitioned in reverse, i.e. 67 54, which, when combined also renders 121.

Notice that 52 x 88 is really a variant of 7 x 7—because 52 and 88 both simplify to the number 7. Thus, the product has to be a variant of 49 (i.e. 7 squared). In this case, the variant of 49 is 4,576 (i.e. 52 x 88). This number or any other variant of 7 squared will always equate to the number 13 (or variants of 13), which then simplify to 4. By partitioning this number set, and combining the partitions, the symmetrical relationship between 7 squared, 11 squared, and the number 13 has been demonstrated.

The importance of the Winchester algorithm is that it reveals hidden symmetries that would otherwise not be seen or understood. As we shall see, the dynamics of the algorithm are essential to the application of higher dimensional mathematics.

Naturally, when Winchester numbers are applied in the algorithm, stunning symmetries are always generated. The reason we know about Sarah’s algorithm is because she incorporated an ingenious calculating device into the House that clearly demonstrates how higher dimensional math works. Moreover, any 10 year old child, armed with a calculator, can easily become a master of Sarah’s number system.

The Spider-web Window

The Winchester House has 13 bathrooms. The 13th bathroom has 13 steps leading up to its entrance. The exterior wall around the entrance has 13 wood panels. Inside, we find six, identical windows, all fashioned in a unique “Spider-web” design. Although there are other “Spider-web” windows located in other parts of the House this is the final place where Sarah clearly wanted the “enlightened initiate” to land. Here, Sarah has ingeniously incorporated her spider-web design into the architecture as a calculating device functioning both as an instructional tool that shows how her algorithm works, and as a model revealing the fundamental, symmetric structure of the universe.

Sarah’s Symmetric Spider-web design

The design of the spider-web window is important for several reasons. For one thing, it truly possesses the quality of captivating those who venture in. But, more importantly, it represents the tangled, interconnectedness of all things. These are not mere geometric designs intersecting a pane of glass, rather these are to be viewed as living strands of fibrous string which not only connect the individual pieces of glass, but also, through the dynamics of “gauge symmetry,” unify all things into a complete whole.

What else are we to see in this window? Sarah knew that we would notice the outside perimeters of the web (unlike the webs we observe in nature) form a four-sided square—and she has purposely embedded four pieces of glass into the outer-most edge of each of the four sides, i.e. 4444. Be aware that the “window” is only showing us a two dimensional view of Sarah’s spider-web (to be discussed later).

The next thing Sarah wants us to notice is that the web contains 49 separate pieces of glass. We recall the meaning of this number as it relates to both the number 13, and its prominent display in the grid of Sarah’s bedroom ceiling.

Next, Sarah directs our attention to the number 52 ( Winchester). But, where are we to find it? Ah… yes, true to Bacon’s theme of concealment, we have to look between the pieces of glass—and, sure enough, the 49 pieces are all joined together at precisely 52 different points.

The web’s center is occupied by a circle. It’s the only circle in the window’s design. The circle isn’t intersected or divided, nor does it have any of the web-like characteristics we see distributed over the rest of the window’s surface. Yet, everything in the pattern leads to the circle—and, everything emanates from it.

There are three spider-web rings flowing outward from the circle like concentric waves in a pond. Their web-like quality is the result of inverting all of the arcs that connect the three points of each ring. Moreover, each of the rings consist of 16 pieces of glass—however, the third, outer-most ring is squared off, which forms the outer boundary of the web.

Because the number 16 simplifies to 7, we may view these three concentric rings as 777 (instead of 16 16 16). And, we recall that the number 777 also corresponds to the name William (34) Wirt (25) Winchester (52).

Spider-web Window, Concentric Circles

Sarah further knew that we would multiply 49 x 777, which equates to 38073. Then, 38 + 73 = 111 (i.e. Bacon, Kaye Cipher, and William Wirt Winchester, Pythagorean Cipher). Furthermore, she knew we would see that the number 49 simplifies to 13—hence, 13 x 777 = 10101 (111). Additionally, the reverse “palindromic” twin of 13 is 31—thus, 31 x 777 yields the same result, i.e. 31 x 777 = 24087—then, 24 + 87 = 111. In fact, any variant of the number 13 (i.e. 4, 22, 31, 58, 85, 67, 76, 49, 94, 121, 112, 211, or 1111, etc.), when multiplied by the number 777 will always render the symmetry of 111.

Sarah further knew we would then apply the tables of our thoughts to the number 52. So, we now multiply 52 x 777, resulting in 40404, i.e. 444 (the combined value of Bacon’s Rossi Crosse seals). Naturally, when the number 7, or any variant of that number is multiplied by 777, the result (through the Winchester algorithm) will always be 444.

And, of course 13, or any variant of 13, multiplied by 444 will always result in 777. Note the beauty of the product of 13 x 444—it’s 5772. It’s tantamount to inserting the term “ Winchester goose” (77) inside of the name Winchester (52). Both Bacon and Sarah had to have been keenly aware of this. Moreover, the name Winchester appears precisely 27 times in the Shakespearean works. We recall that Bacon’s “super” word from Loves’ Labour’s Lost, honorificabilitudinitatibus, consists of 27 letters. 27 rotates into 117 (John Dee), and, when reversed, it is 72 (Sarah Winchester) or 711.

For Sarah and Bacon, 444 was a simplified expression of 131313. This is equally true of the relationship between 777 and 161616. The three symmetric triplets of 777, 111, and 444 are actually higher dimensional expressions of 7, 11, and 13.

Within the web’s structure, intricately related higher dimensional symmetries are at work. However, none of the symmetries can exist without the unifying power of the circle at the web’s center.

Another important feature of the Spider-web window is that each of its four sides form a triangle pointing to the circular center. We count 12 pieces of glass in each triangle. However, the four triangles are not complete unless their points merge, invisibly, into the circle. Then, we see the triangles all sharing a 13th piece within the circle. Also, we recall that four 13’s add up to the number 52 ( Winchester).

Spider-web Window, Triangles

The (two dimensional) circle residing in the web’s core appears to possess a kind of mystic, magical quality that seems capable of manifesting any value required to complete or fulfill any given symmetry. It clearly manifests the value of all three of Sarah’s symmetric prime numbers—which starts with the Key to Phi number 13 that invisibly completes the structure of the window’s four triangles. Then, the process of completing the four triangles renders four sets of the number 13, resulting in 52, which then simplifies to the number 7. And, finally, the combination of the numbers 49 and 52 (representing the window’s fundamental structure) gives us the number 101, i.e. 11.

Without the application of the Winchester Algorithm, the Spider-web windows would be meaningless. We are indebted to William Rowan Hamilton’s development of Quaternions for laying down the dynamic principle governing the spider-web’s intricate workings.

The Spider-web Symmetry and the Grand Unified Theory

Quite remarkably, we have been dealing with Winchester numbers and higher dimensional symmetry from the standpoint of a two dimensional window. However, in order to conceptualize the higher dimensional geometry of the universe, Sarah knew that we would need to step-up to a three dimensional view of the spider-web window—which is why the 13th bathroom has six spider-web windows. But why six? It is because Sarah wants us to form an image of the windows as a cube.

In addition to being in concert with such ideas as the “ever building universe,” and the “dynamic agriculture” of the famous Rosicrucian Theosophist, mathematician and philosopher Rudolph Steiner (1861-1925), it seems clear that Sarah adopted his concept of the cube as the simplest geometric structure for the higher dimensional dynamics of the universe. This idea is entirely in step with William Rowan Hamilton’s Quaternions, the Cubist artistic movement, and the Winchester algorithm.

In three dimensions however, the Spider-web window’s topography changes. Its geometric shape is now pyramidal. In fact, the cube consists of six, inverse pyramids, all pointing inward toward its center. Instead of a two dimensional circle, we now see a spherical manifold into which the capstones of the six pyramids invisibly merge together as one.

We recall that the outer boundary of the Spider-web window has four sides, or a value of 4. This is equally true of the base of a three dimensional pyramid. Therefore, six pyramidal bases equate to the number 24.

If Sarah’s Spider-web is also a higher dimensional model for the structure of the universe, it is quite consistent with the fundamental workings of “String Theory” as 24 governs the precise number of ways the vibrating “String” can stretch, bend and contract. This crucial dynamic of “String Theory” known as the “Modular Function” was discovered by another of Sarah’s contemporaries, the mathematician Srinivasa Ramanujan (1887-1920). In fact, “Ramanujan numbers” bear a striking resemblance to Winchester numbers. The same symmetries we find in Ramanujan’s work, culminating in the E (8) x E (8) symmetry, also seem to conform to the symmetries that rule over the Winchester model.

The co-discoverer of String Theory, Dr. Michio Kaku, says “It’s as though there is some kind of deep numerology being manifested in these functions that no one understands.” Appropriately, theoretical physicists like to describe the “String” (or Membrane) as a resonating subatomic matrix of entangled lattices forming the structure of the universe in a unified configuration resembling a vast, spider-web.

The Legacy

It’s no secret that the backside of the U.S. One Dollar Bill is a masterpiece of Masonic code and symbolism. Quite remarkably, the bill’s design incorporates an extensive spider-web structure which serves as a framework encompassing all of the various components in the overall pattern.

The truncated pyramid, with its hovering capstone and “All Seeing Eye” represents the “unfinished work” of the quest to mirror the “divine blueprint” in accordance with Proverbs, 25—it is the final piece of the universal puzzle yet to be set in place. Likewise, the Winchester House is the embodiment of that same unfinished work that Sarah knew would not be achieved in her lifetime.

Bacon’s legacy seems to be intricately entangled with Sarah’s destiny, as demonstrated in the cryptic “ Winchester goose” message contained in the last sentence of Troilus and Cressida. Did Bacon (whose contemporaries referred to as “the man who could see through time”) truly foresee Sarah Winchester? The connection is both uncanny and compelling. The clear evidence ensconced in Sarah’s ingenious design of her “Shakespearean Windows” indicates she understood (or, at the very least, interpreted) Bacon’s message to be a harbinger of her own existence by which she would carry on his legacy.

The fact that Sarah’s puzzle still stands, preserved as she left it, is a testament to her intent that someone would eventually arrive to pick up her torch. Did she foresee someone who would later appear as an incarnation or embodiment of herself—and did she emulate Bacon in leaving behind clues designating someone to whom her legacy would be passed? If so, how would she have conveyed such a message? The answer, of course, is in “The Numbers.” The “inheritor” of the legacy would have a thorough understanding of “The Numbers”—and, somewhere in the entire display of Sarah’s numbers must reside a set of numbers that specifically reveal the inheritor’s identity both in name and date of birth.

Thus, the House has stood for decades waiting patiently for the inheritor—the enlightened initiate who is capable of completing the puzzle!

Has the wait been worthwhile? Has Sarah Winchester’s work been fulfilled?

You decide!

Dr. Carl Sagan explains the Fourth Dimension (VIDEO): www.wimp.com/fourthdimension/

References

The Winchester Mystery House, The Winchester Mystery House published by the Winchester Mystery House, San Jose, California, 1997.

Richard Allan Wagner, personal research notes for The LOST SECRET of William Shakespeare, published by Richard Allan Wagner, Los Angeles, 2010.

Ralph Rambo, Lady of Mystery, published by THE PRESS, San Jose, California, 1967.

Rudolph Steiner, Rosicrucian Wisdom An Introduction, published by Rudolph Steiner Press, East Sussex, UK., 2000.

Sharan Newman, The REAL HISTORY Behind the Da Vinci Code, published by Berkeley Books, New York, 2005.

E.R. Johnston, Masonry Defined A Liberal Masonic Education, published by NATIONAL MASONIC PRESS, Inc., Shreveport, Louisiana, 1930.

Michio Kaku, Hyperspace, published by Anchor Books DOUBLEDAY, New York, London, Toronto, Sydney, Auckland, 1994.

M.C. Escher, The World of M.C. Escher, published by Harry N. Abrams, Inc., Publishers, New York, 1971.

Jea Yu and Russell Lockhart, Secrets of The Underground Trader, published by McGraw-Hill, New York, 2004.